2007海南高考,2007海南高考分数

1.2007年新课标文科数学高考题

2.专家谈2007高考英语：考场上妥善安排做题时间

2007年高考各省份难度排行榜

1、地狱模式：江苏、浙江、河北、山东。

难度系数：★★★★★

理由分析：江苏总分480分，只考语数外，但是名校录取不仅看分数线，还看选测科目等级，如果考了一个B，那么很抱歉，与一流高校基本无缘了。

浙江因为实施新高考3+3模式，尝试了全新的选科、选考，最终结果一言难尽，看看最后一分段分数线、高分段人数及清北录取人数，就能了解一二。

河北、山东两个难兄难弟，本省高分段人数多，高考人数多，竞争压力非常大，尤其是河北。

2、噩梦模式：湖南、湖北、河南。

难度系数：★★★★

理由分析：两湖的考生都属于低调而强大的类型，河南每年高考人数都位居全国前列，本省除了一一个郑州大学，又没有其他重点大学支撑，导致本省高考竞争非常激烈。

3、困难模式：安徽、江西、山西、广东、四川。

难度系数：★★★

理由分析：这些省份的高考录取率一般位居中游，各地高中的教育教学模式也有共同之处。有些省份的考生努力考到省外尤其是北上广的大学，成了顶尖大学最大的生源基地。

而广东在全国教育分布中，属于相对丰富的省份，但由于每年考生基数大、流动人口多，所以广东的高考难度系数属于第别。

高考难度一般的省份

一般模式：陕西、辽宁、吉林、黑龙江、内蒙古、福建、重庆、贵州、甘肃、云南。

难度系数：★★

理由分析：主要是东北地区及西部地区省份，陕西是高考大省，但好在省内较好的本科院校比较多；辽宁也是优质大学数量较多的省份；其他省份的考生人数较少，考生的选择和回旋余地都比较大。

较易模式：北京、上海、天津、青海、***、西藏、海南、宁夏、广西。

难度系数：★

理由分析：北_上天这类自主命题和高考改革的省份，试题常常引领趋势，录取模式也是独树一帜；由于当地教育丰富，往往当地考生不需要太高的分数便可被优质大学录取。

2007年新课标文科数学高考题

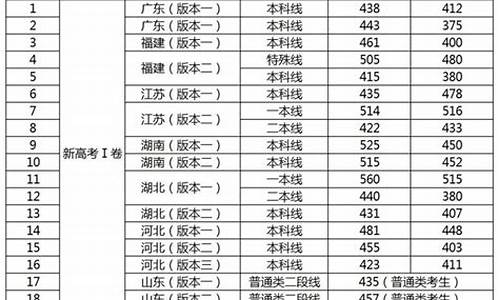
2007年河南高考分数线如下：

以北京市为例，该地区2006年的本科一批文史分数线是516分、二批476分、三批442分；本科一批理工分数线是528分、二批476分、三批442分。海南省2006年的本科一批文史分数线是613分、二批559分；本科一批理工分数线是569分、二批518分。

上海市2006年的本科一批文史分数线是490分、二批450分；本科一批理工分数线是466分、二批412分。四川省本科一批文史分数线是550分、二批502分、三批478分；本科一批理工分数线是560分、二批512分、三批485分。

高考分数线以及投档线设定规则：

1、录取最低控制分数线由各省、自治区、直辖市分别划定，由于条件各异，分数线的分差可能很大，最高与最低相差超过100分。

2、根据当年招生和考生成绩，依据人数来划定。一般按略多于数划定，多数是数的1.1-1.2倍，全省考生按考分的高低排下来，排到该人数时的分数，即当年该省的最低控制分数线，只有达到该分数的考生才有资格被录取。

3、投档分数线，一般是按招生数1：1.2以内的比例投档确定。同一批录取的院校中，投档分数线是不一致的，高低由各校的生源情况决定。生源好的高校投档分数线可能高出控制分数线很多，生源不好的则低一些，但原则上它不能低于同批次录取控制分数线。

专家谈2007高考英语：考场上妥善安排做题时间

孩子，07年的新课标卷是宁夏海南卷。

2007年普通高等学校招生全国统一考试

文科数学（宁夏、 海南卷）

本试卷分第I卷（选择题）和第II卷（非选择题）两部分．第II卷第22题为选考题，其他题为必考题．考生作答时，将答案答在答题卡上，在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回．

注意事项：

1．答题前，考生先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上

的准考证号、姓名，并将条形码粘贴在指定位置上．

2．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂基他答案标号，非选择题答案使用毫米的黑色中性（签字）笔或炭素笔书写，字体工整、笔迹清楚．

3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．

4．保持卡面清洁，不折叠，不破损．

5．作选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的标号涂黑．

参考公式：

样本数据，，，的标准差 锥体体积公式

其中为标本平均数 其中为底面面积，为高

柱体体积公式 球的表面积、体积公式

，

其中为底面面积，为高 其中为球的半径

第Ⅰ卷

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，

只有一项是符合题目要求的．

1．设集合，则（　　）

A． B．

C． D．

解析由,可得.

答案：A

2．已知命题，，则（　　）

A．， B．，

C．， D．，

解析是对的否定，故有：

答案：C

3．函数在区间的简图是（　　）

解析排除B、D，排除C。也可由五点法作图验证。

答案：A

4．已知平面向量，则向量（　　）

A． B．

C． D．

解析

答案：D

5．如果执行右面的程序框图，那么输出的（　　）

A．2450 B．2500

C．2550 D．2652

解析由程序知，

答案：C

6．已知成等比数列，且曲线的顶点是，则等于（　　）

A．3 B．2 C．1 D．

解析曲线的顶点是，则：由

成等比数列知，

答案：B

7．已知抛物线的焦点为，点，

在抛物线上，且，则有（　　）

A． B．

C． D．

解析由抛物线定义，即：．

答案：C

8．已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），

可得这个几何体的体积是（　　）

A． B．

C． D．

解析如图，

答案：B

9．若，则的值为（　　）

A． B． 　C． D．

解析

答案：C

10．曲线在点处的切线与坐标轴所围三角形的面积为（　　）

A． B． C． D．

解析：曲线在点处的切线斜率为，因此切线方程为则切线与坐标轴交点为所以：

答案：D

11．已知三棱锥的各顶点都在一个半径为的球面上，

球心在上，底面，，

则球的体积与三棱锥体积之比是（　　）

A． B． C． D．

解析如图，

答案：D

12．甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表

甲的成绩

环数 7 8 9 10

频数 5 5 5 5

乙的成绩

环数 7 8 9 10

频数 6 4 4 6

丙的成绩

环数 7 8 9 10

频数 4 6 6 4

分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有（　　）

A． B．

C． D．

解析

答案：B

第Ⅱ卷

本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题为选考题，考生根据要求做答．

二、填空题：本大题共4小题，每小题5分．

13．已知双曲线的顶点到渐近线的距离为2，焦点到渐近线的距离为6，

则该双曲线的离心率为　　　　　．

解析如图，过双曲线的顶点A、焦点F分别向其渐近线作垂线，垂足分别为B、C，

则：

答案：3

14．设函数为偶函数，则　　　　．

解析

答案：-1

15．是虚数单位，　　　　　．（用的形式表示，）

解析

答案：

16．已知是等差数列，，其前5项和，则其公差　　　　．

解析

答案：

三、解答题：解答应写出文字说明，证明过程或演算步骤．

17．（本小题满分12分）

如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个测点与．现测得，并在点测得塔顶的仰角为，求塔高．

解析在中，．

由正弦定理得．

所以．

在中，．

18．（本小题满分12分）

如图，为空间四点．在中，．

等边三角形以为轴运动．

（Ⅰ）当平面平面时，求；

（Ⅱ）当转动时，是否总有？

证明你的结论．

解析（Ⅰ）取的中点，连结，

因为是等边三角形，所以．

当平面平面时，

因为平面平面，

所以平面，

可知

由已知可得，在中，．

（Ⅱ）当以为轴转动时，总有．

证明：

（ⅰ）当在平面内时，因为，

所以都在线段的垂直平分线上，即．

（ⅱ）当不在平面内时，由（Ⅰ）知．又因，所以．

又为相交直线，所以平面，由平面，得．

综上所述，总有．

19．（本小题满分12分）设函数

（Ⅰ）讨论的单调性；

（Ⅱ）求在区间的最大值和最小值．

解析的定义域为．

（Ⅰ）．

当时，；当时，；当时，．

从而，分别在区间，单调增加，在区间单调减少．

（Ⅱ）由（Ⅰ）知在区间的最小值为．

又．

所以在区间的最大值为．

20．（本小题满分12分）设有关于的一元二次方程．

（Ⅰ）若是从四个数中任取的一个数，是从三个数中任取的一个数，

求上述方程有实根的概率．

（Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，

求上述方程有实根的概率．

解析设为“方程有实根”．

当，时，方程有实根的充要条件为．

（Ⅰ）基本共12个：

．

其中第一个数表示的取值，第二个数表示的取值．

中包含9个基本，发生的概率为．

（Ⅱ）试验的全部结束所构成的区域为．

构成的区域为．

所以所求的概率为．

21．（本小题满分12分）

在平面直角坐标系中，已知圆的圆心为，过点

且斜率为的直线与圆相交于不同的两点．

（Ⅰ）求的取值范围；

（Ⅱ）是否存在常数，使得向量与共线？如果存在，求值；

如果不存在，请说明理由．

解析（Ⅰ）圆的方程可写成，所以圆心为，过

且斜率为的直线方程为．

代入圆方程得，

整理得．　　　①

直线与圆交于两个不同的点等价于

解得，即的取值范围为．

（Ⅱ）设，则，

由方程①，

②

又．　　　　③

而．

所以与共线等价于，

将②③代入上式，解得．

由（Ⅰ）知，故没有符合题意的常数．

22．请考生在A、B两题中任选一题作答，如果多做，则按所做的第一题记分．作答时，

用2B铅笔在答题卡上把所选题目对应的标号涂黑．

22．A（本小题满分10分）选修4－1：几何证明选讲

如图，已知是的切线，为切点，是的割线，与

交于两点，圆心在的内部，点是的中点．

（Ⅰ）证明四点共圆；

（Ⅱ）求的大小．

解析（Ⅰ）证明：连结．

因为与相切于点，所以．

因为是的弦的中点，所以．

于是．

由圆心在的内部，可知四边形的对角互补，

所以四点共圆．

（Ⅱ）解：由（Ⅰ）得四点共圆，所以．

由（Ⅰ）得．

由圆心在的内部，可知．

所以．

22．B（本小题满分10分）选修4－4：坐标系与参数方程

和的极坐标方程分别为．

（Ⅰ）把和的极坐标方程化为直角坐标方程；

（Ⅱ）求经过，交点的直线的直角坐标方程．

解析以有点为原点，极轴为轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位．

（Ⅰ），，由得．

所以．

即为的直角坐标方程．

同理为的直角坐标方程．

（Ⅱ）由

解得．

即，交于点和．

过交点的直线的直角坐标方程为．

海南中学高级教师谭虎啸从事高中英语教学工作20年，是该校英语教研组副组长，被北大提前录取后又被美国麻省理工学院录取的07届考生傅杰运，就是他的学生。

　谭老师认为，在临近高考的这段时间，适当增加阅读量，做些针对性的练习有助于考场发挥。而做完形填空的题目时，很多学生面对四个词性一样的词汇时可能感到困惑，从语法上判断四个词可能都没有错，这时就要掌握答题的技巧了。考生做这种题目，别把自己当成局外人，要设自己是文章的主人公，带着他的情感和态度，设想自己正处在当时的情景之中，就会做出正确的判断说出正确的话，做出正确的举动。

　在临近高考的几周内，谭老师建议学生适当做些套题，做题时要留心发现问题，再做些针对性的练习。为了做适应性的调整，考前最后的两三天也不要放弃学英语，要根据高考时英语考试的时间安排，在限定时间内做一套试卷。

　在应试技艺方面，谭老师强调，高考考场上时间极为宝贵，根据历年高考经验，考场上遇到难到实在无能为力的题，宁可放弃也不能耽误太多时间。做单选题所耗时间不要太久，10分钟左右就可以。如果考生开始做题太仔细、太慢，到后面就会因时间紧迫，压力太大。做完形填空题，应该安排17-18分钟；做阅读题包括阅读信息填空应该安排45分钟之内；改错题该安排7-8分钟；写作题至少安排15分钟。在整体上要保持做题的节奏，才能充分发挥自己的实力，不会因为时间仓促而失去该得的分，这点非常重要。